PPO
Introduction
The Proximal Policy Optimization (PPO) algorithm, proposed by OpenAI in 2017 [1], establishes a robust policy gradient framework that combines three core components: clipped objective functions, value estimation, and entropy regularization.
Objective Function
The unified optimization objective integrates three key elements:
\[L_t^{\text{CLIP+VF+S}}(\theta) = \mathbb{E}_t \left[ L_t^{\text{CLIP}}(\theta) - c_1 L_t^{\text{VF}}(\theta) + c_2 S[\pi_\theta](s_t) \right]\]1. Clipped Surrogate Objective
\[L_t^{\text{CLIP}}(\theta) = \mathbb{E}_t \left[ \min\left( r_t(\theta) \hat{A}_t,\ \text{clip}\left( r_t(\theta),\ 1-\epsilon,\ 1+\epsilon \right) \hat{A}_t \right) \right]\]where $r_t(\theta) = \frac{\pi_{\theta}(a_t \mid s_t)}{\pi_{\text{old}}(a_t \mid s_t)}$ is ratio paremeter, $\hat{A}_t$ is advantage estimate and $\epsilon \in [0.1, 0.3]$ a clipping threshold which contrains policy update in a safe limit.
2. Value Function Loss
\[L_t^{\text{VF}}(\theta) = \frac{1}{2} \mathbb{E}_t \left[ \left( V_\theta(s_t) - V_t^{\text{targ}} \right)^2 \right]\]Implementation Note: The $\frac{1}{2}$ coefficient serves as a gradient scaling factor.
3. Entropy Regularization
\[S[\pi_\theta](s_t) = -\sum_{a'} \pi_\theta(a'|s_t) \log \pi_\theta(a'|s_t)\]Tips:
Coefficients $c_1$ and $c_2$ balance the policy update, value function accuracy, and entropy bonus. Usually value loss weight is set to $c_1 \in [0.5, 1.0]$ and entropy bonus weight is $c_2 \in [0.01, 0.05]$.
Architecture & Execution Pipeline
Network Architecture Components
The policy network $\pi_\theta(a|s_t)$ and value function estimator $V_\theta(s_t)$ share a unified neural architecture with sepecialized components such as feature encoder $h_t=f_\theta^{encoder}(s_t)$ with separate heads, e.g. policy head with $\pi_\theta(a|s_t)={\rm softmax}(W_\pi h_t+b_\pi)$ and output probability distribution over action $\mathcal{A}$ while value head maybe $V_\theta(s_t)=W_vh_t+b_v$ with a scalar value estimate.
Execution Workflow
Phase 1: Experience Collection Pipeline
During the rollout phase, agents interact with the environment using the old policy $\pi_{\text{old}}$ to generate trajectories \(\tau=\{(s_t, a_t, r_t)\}_{t=0}^{T-1}\). Subsequently, the Generalized Advantage Estimation (GAE) method computes advantage values $\hat{A}_t$ through recursive temporal difference calculations:
\[\begin{aligned} \delta_t &= r_t + \gamma V_\theta(s_{t+1}) - V_\theta(s_t), \\ \hat{A}_t &= \sum_{\ell=0}^{T-t-1} (\gamma\lambda)^\ell \delta_{t+\ell}, \end{aligned}\]where $\gamma$ is the discount factor and $\lambda$ the GAE smoothing coefficient. Processed transitions \((s_t, a_t, \hat{A}_t, V_t^{\mathrm{targ}})\) — with target values \(V_t^{\mathrm{targ}}=\hat{A}_t+V_\theta(s_t)\) — are stored in an experience replay buffer (capacity: $10^5 \sim 10^6$). This staged pipeline decouples data collection from policy updates while maintaining sample diversity through large-scale experience reuse.
Phase 2: Parameter Update
For $K$ optimization epochs:
-
Mini-batch Sampling: Uniformly sample $B$ transitions ($B \in [64, 2048]$) from buffer.
-
Policy Optimization: Compute gradients for the clipped surrogate objective: \(\nabla_\theta L^{CLIP}=\mathbb{E}_t\left[\min\left(r_t(\theta)\hat{A}_t, {\text clip}(r_t(\theta), 1-\epsilon, 1+\epsilon)\hat{A}_t\right)\nabla_\theta\log\pi_\theta(a_t|s_t)\right]\)
-
Value Network Update: Minimize the value function’s MSE loss through SGD: \(\nabla_\theta L^{VF}=\mathbb{E}_{(s_t, V_t^{\text targ})\sim {\text buffer}}\left[(V_\theta(s_t)-V_t^{\text targ}\nabla_\theta V_\theta(s_t))\right]\)
-
Entropy Adaptation (Optional): Dynamically adjust $c_2$ based on entropy monitoring.
Applications
This part will show some applications with PPO including Reinforcement Learning from Human Feedback (RLHF)[2] as well as Atari games.
RLHF
RLHF is introduced to further align an LLM to human values. In this part, I attempt to show the details of implementation of RLHF with PPO, including:
- The data workflow of RLHF
- The mainstream framework
- Examples
The data workflow of RLHF
PPO-based RLHF system typically consists of 4 LLMs: an actor, a critic, a reference policy network and a reward model. PPO-based RLHF proceeds in iterations, each with 3 stages:
- response generation using the actor model with a batch of prompts
- preparation of training data by scoring the generated response through a single forward pass of the critic, reference policy and rewards models
- learning from human preference by updating actor and critic through and backward computation.
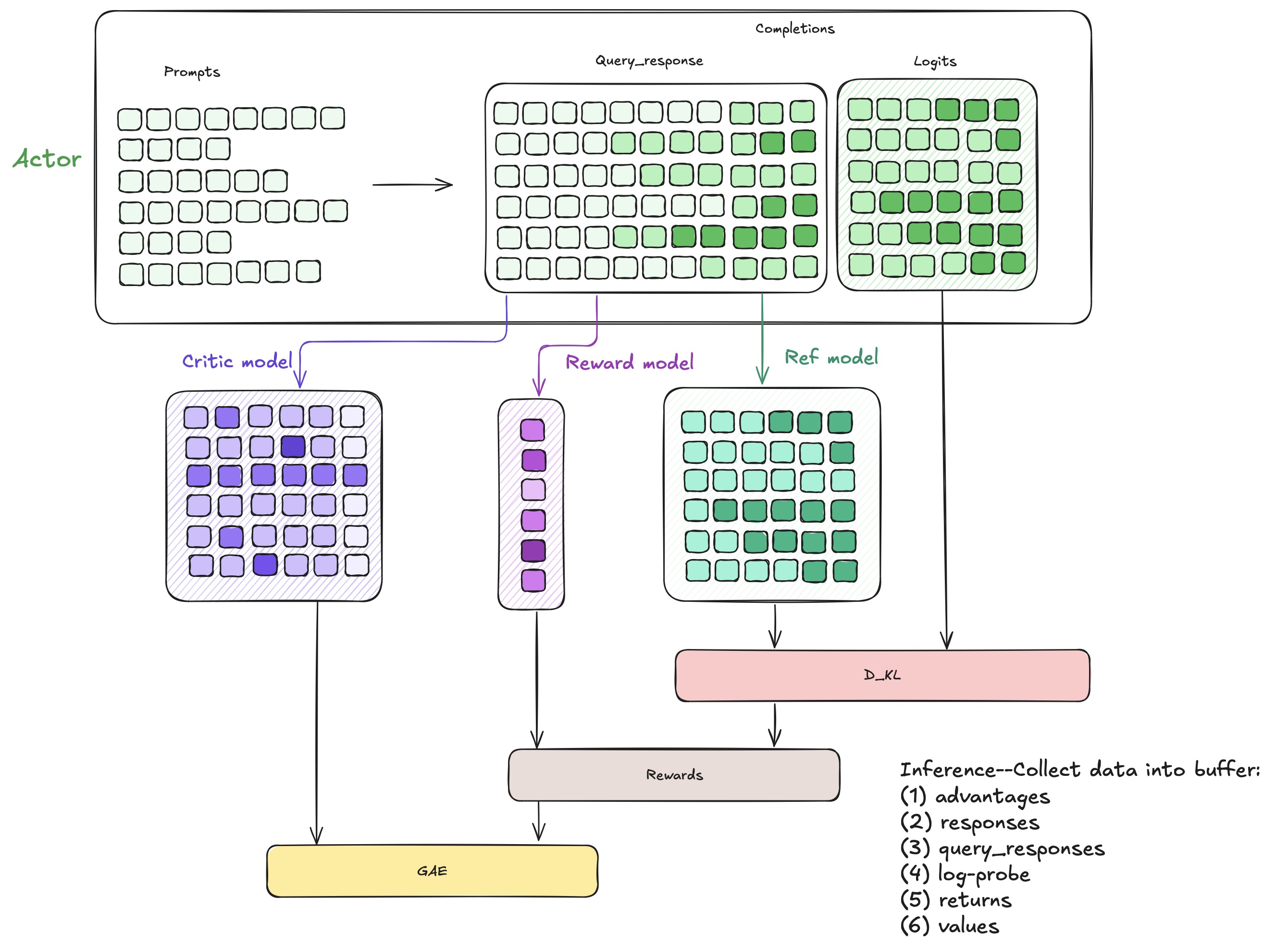
After inference, we have collected some data which will be stored into buffer:
- logprob (from actor)
- ref_logprob (from reference model)
- rewards (token-level rewards, consists of kl (logprobs - ref_logprobs) and scores generated by reward model)
- values (from critic)
- token-level advantages
During training, we sample data from buffer and update actor and critic by PPO methods.
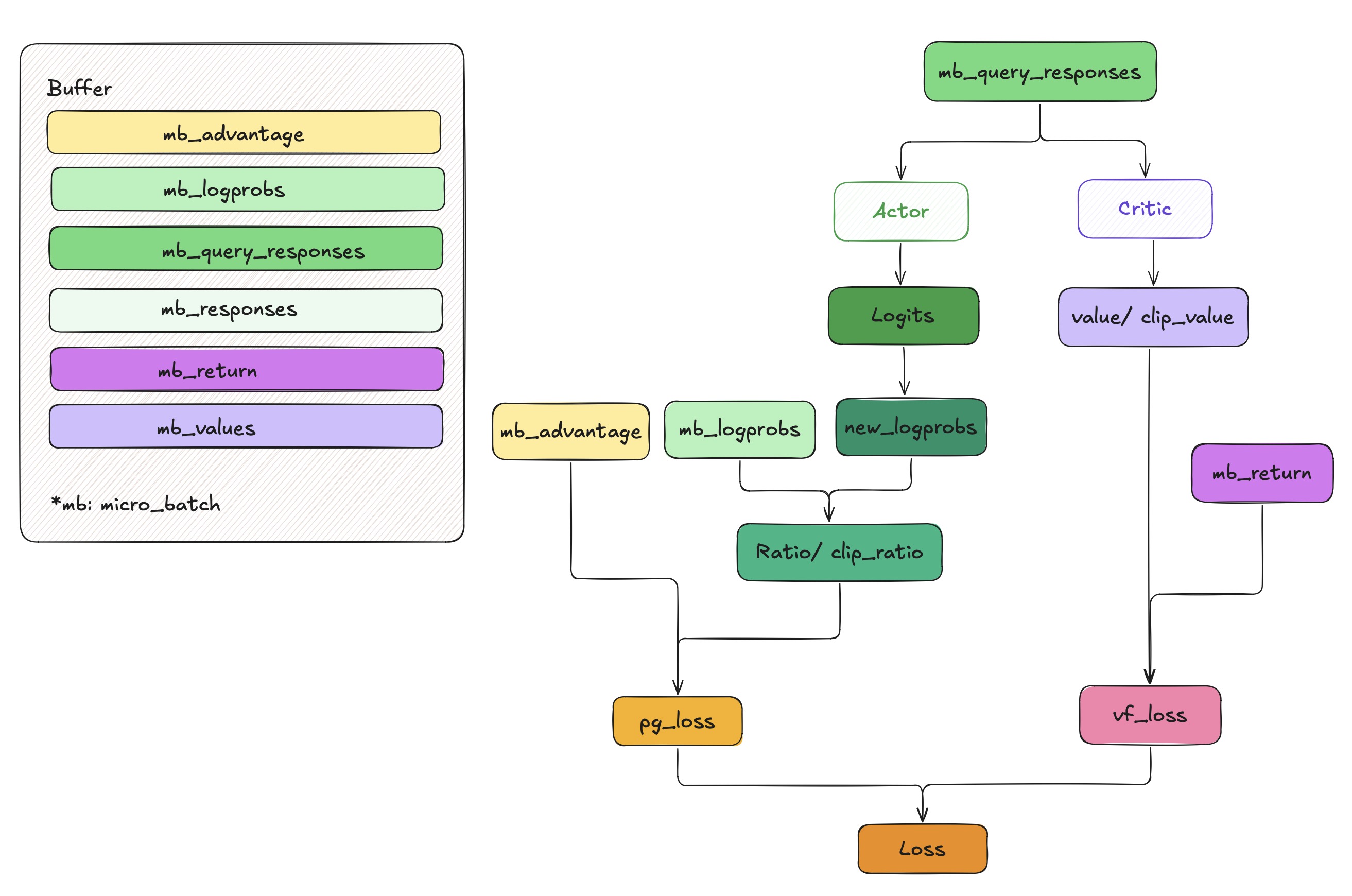
The mainstream framwork
1. TRL
From my perspective, TRL [3] is a comprehensive and user-friendly library to post-train foundation models. There exists many advanced techniques like Supervised Fine-Tuning (SFT), Proximal Policy Optimization (PPO) and Group Relative Policy Optimization (GRPO) and so on.
For initial implementation, I strongly recommend reading the Official PPO Trainer Documentation.
Here, I aim to highlight the core computation codes, which will help you gain a deeper understanding of PPO in the RLHF (Reinforcement Learning from Human Feedback) scenario. For comprehensive implementation details, refer to the canonical guide: The N Implementation Details of RLHF with PPO [4].
- How to get scores?
We feed query as well as response into reward model to attain scores. This means that each score of a token is highly dependent on previous tokens. -
How to compute rewards?
\[\mathcal{R}(x,y) = \underbrace{r_\theta(x,y)}_{\text{Reward Model}} - \beta \cdot \underbrace{D_{\text{KL}}\big(\pi_\phi(y|x) \parallel \pi_{\text{ref}}(y|x)\big)}_{\text{Policy Regularization}}\]
Through reward model, we attain scores which is only given at the end of episode (stop_token) with shape(batch_size, 1). But it is not the final reward. Actually, The complete reward function combines supervised signal, policy constraint (trl/trl/trainer /ppo_trainer.py#509) and sometimes penalty to responses which don’t have stop_token: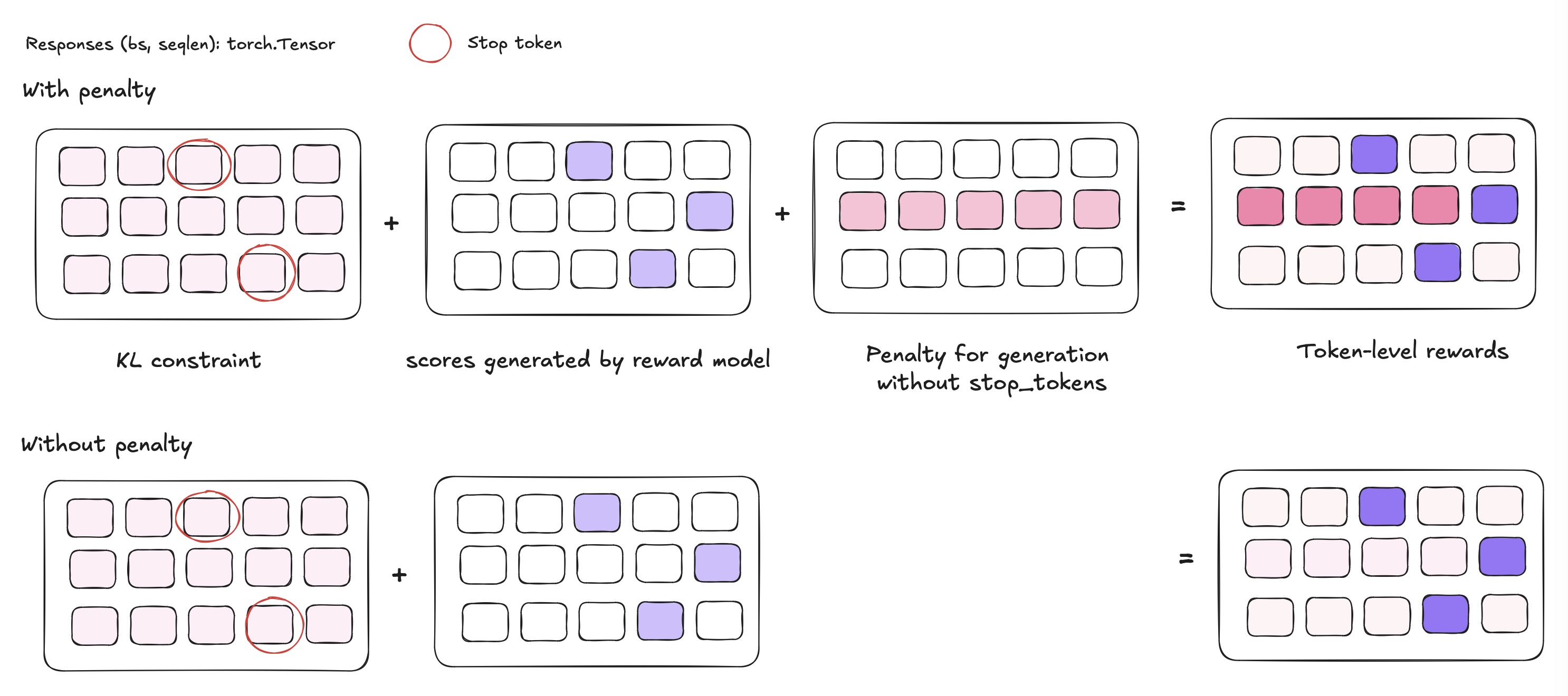
- Scale the logits by sampling temperature
When calculating the log probability of responses, the model first outputs the logits of the tokens in reponses, followed by dividing the logits with the sampling temperature (lm_human_preferences/policy.py#L121) i.e.,logits /= self.temperatureIt is said that without this scaling, the KL would rise faster than expected, and performanc would deteriorate[4].
- Carefully mask scores and logprobs. TRL create attention mask by 3 process
- Truncate responses containing
stop_token_id. - Create index of responses.
- Create mask by comparing index and responses’ length.
- Mask
logprob,ref_modelas well asvalues.
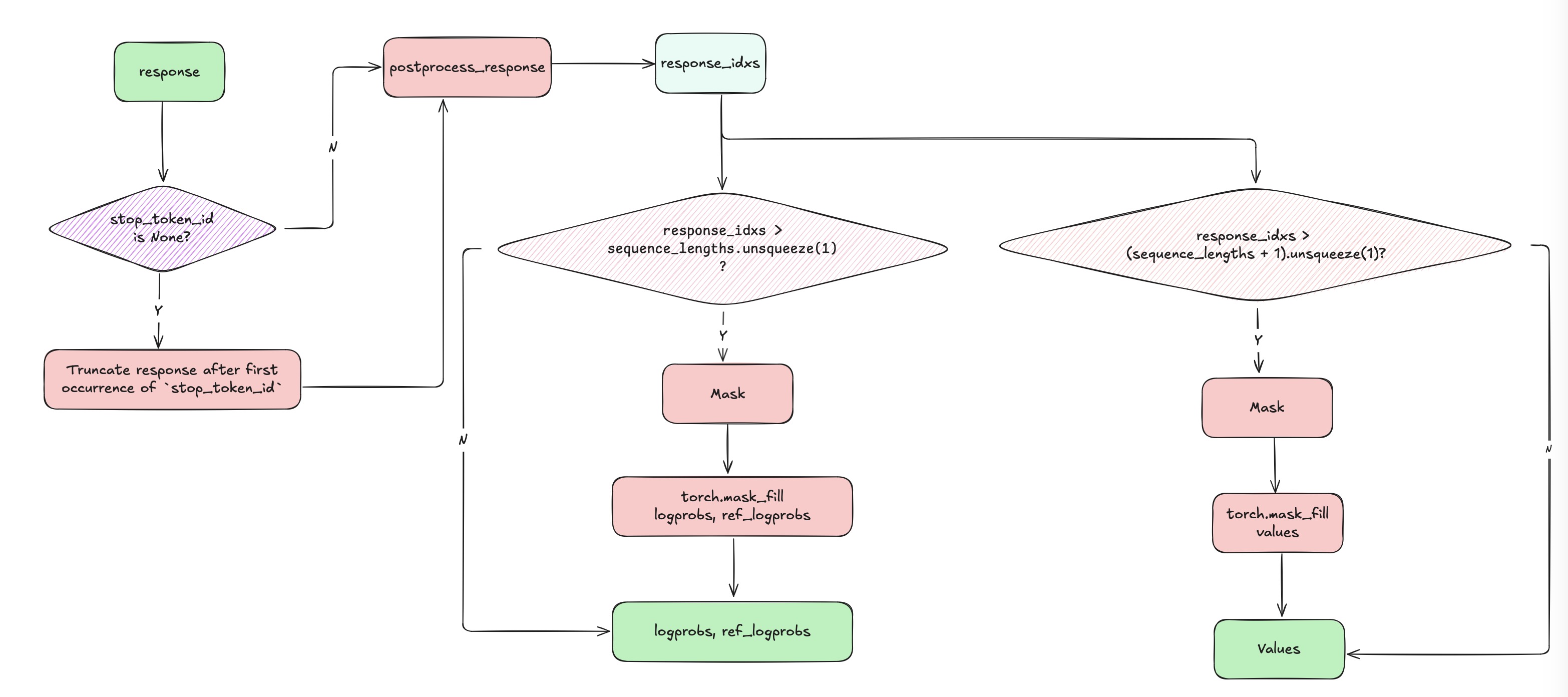
- Truncate responses containing
- Pytorch Adam optimizer numerical issues w.r.t RLHF.
-
During PPO training with
num_total_batchesupdate rounds, how arebatch_size,local_batch_sizeandnum_ppo_epochsinvolved?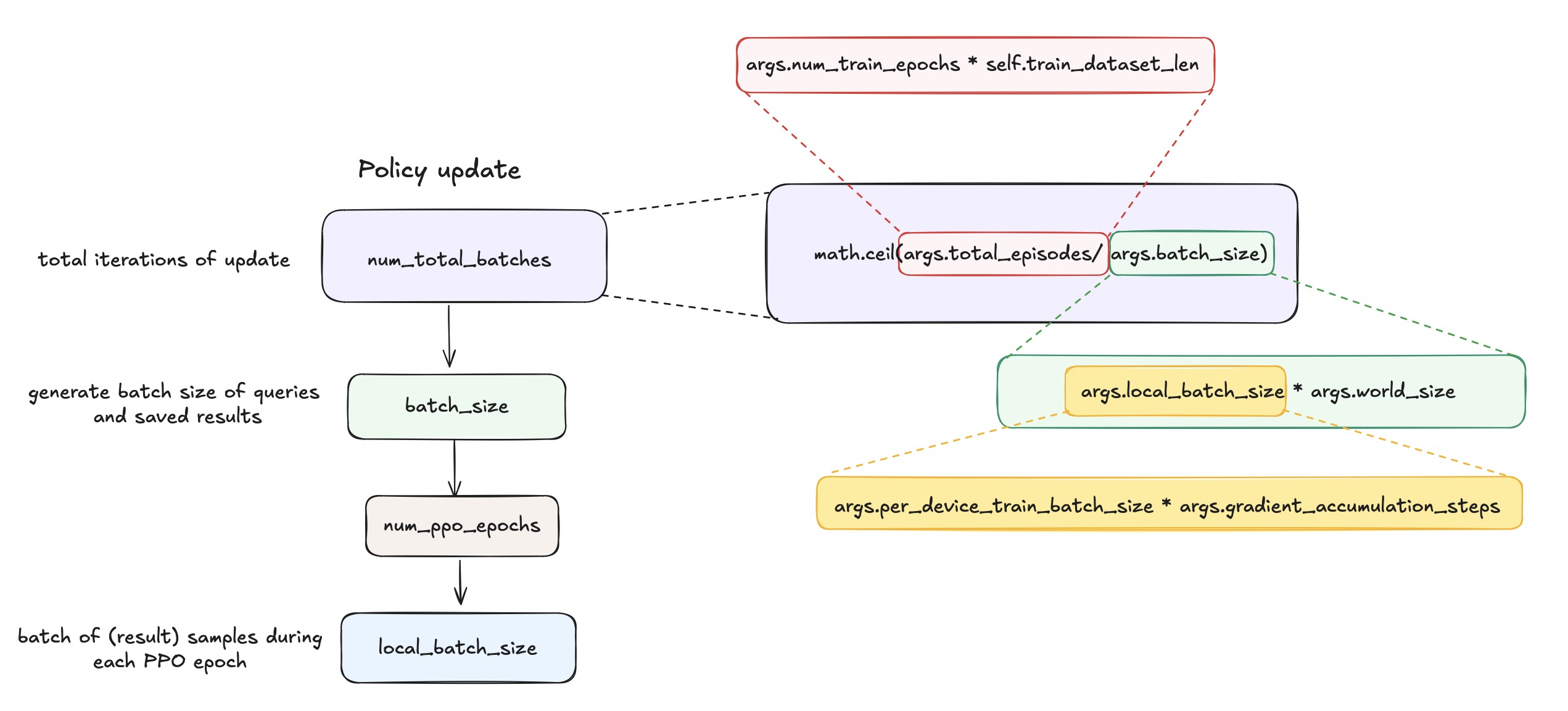
It performs
num_total_batchesof sampling and traing.
In each round:- It samples
local_batch_size * word_sizedata from the environment (i.e.,batch_size). - It then trains this batch
num_ppo_epochstimes, typically with minibatches oflocal_batch_sizeon each device.
- It samples
References
- Schulman, J., Wolski, F., Dhariwal, P., Radford, A., & Klimov, O. (2017). Proximal Policy Optimization Algorithms. arXiv preprint arXiv:1707.06347.
DOI: 10.48550/arXiv.1707.06347 - Yuntao Bai, Andy Jones, Kamal Ndousse, Amanda Askell, Anna Chen, Nova DasSarma, Dawn Drain, Stanislav Fort, Deep Ganguli, Tom Henighan, et al. 2022. Training a helpful and harmless assistant with reinforcement learning from human feedback. arXiv preprint arXiv:2204.05862 (2022).
- https://github.com/huggingface/trl
- The N Implementation Details of RLHF with PPO
- Diederik K. Adam: A method for stochastic optimization[J]. (No Title), 2014.
- https://excalidraw.com/#json=LWnzG4w2k5DjF_EOL_xPt,e2w3a-hFJ_gX5vOfeyXGTw